こんにちは、しんたです。
2023年の旧帝の問題も少しずつ解いています。
今回は東北大学をやってみたので、記事に残しておきます。
感想
今年の東北大は全体的に解きやすい構成でした。
第6問(2)が突出して処理も多く、捨て問になるでしょうが、ほかの問題はいずれも完答したいものでしたから、平均点は高そうです。4完+αくらいが目標になりそうですね。
第1問


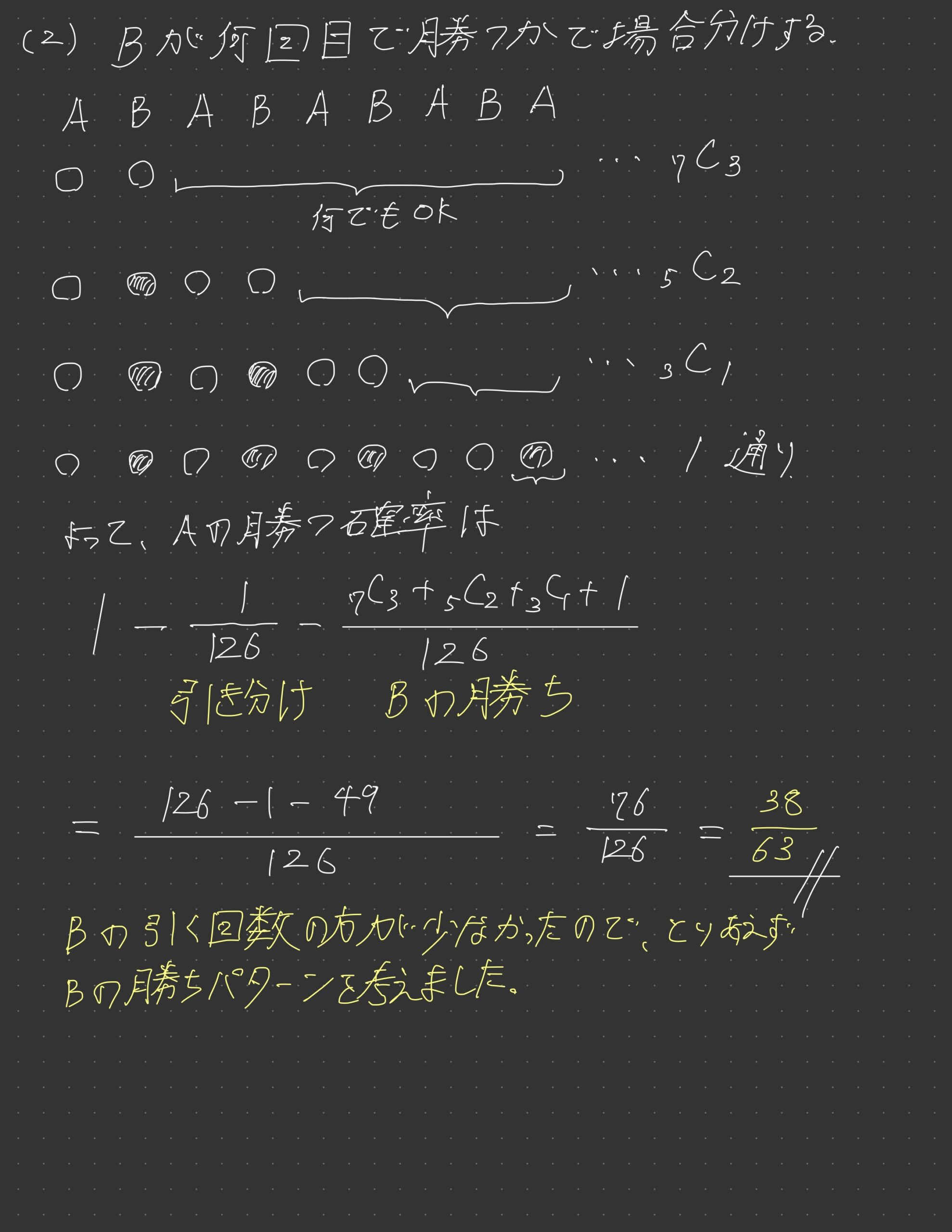
~感想~
実際に勝つパターンを列挙していけば大丈夫な感じでした。
勝ち負けのついた後でも、並べるのを終わらせないで考えると一つ一つの事象は等確率となってくれるため都合がいいですね。
第2問



~感想~
(1)は方程式の解を求めることを考えると積の形が欲しいですので、和積でOKですね。
(2)はガウス記号系の問題でした。
不等式で評価すれば収束先がわかりますね。はさみうちの雰囲気も分かりやすいので、やりやすめなのですかね?
第3問



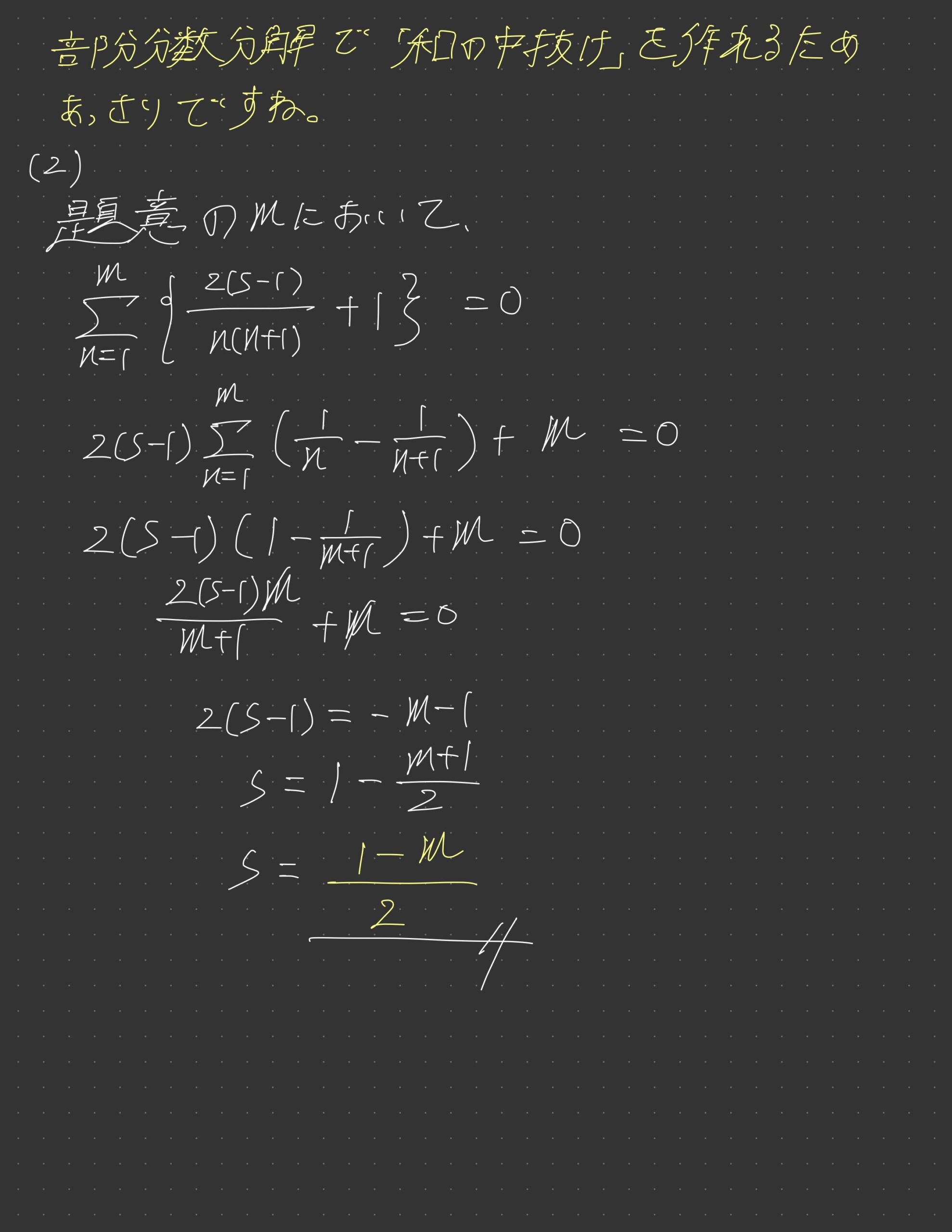
~感想~
(1)は両辺にn+1をかければ綺麗に番号ずらしの形を作れたのですが、なんだか全く気付かなかったので、実際にいくつか値を代入していって一般項を予想して示すという何とも不格好なことになりました。
(2)は自分は(1)で次数を分母の方が大きくなるように処理しておいたため、部分分数分解で和の中抜けを作ることも分かりやすく、スムーズにいきました。(1)ができた人にはサービス問題ですね。
第4問



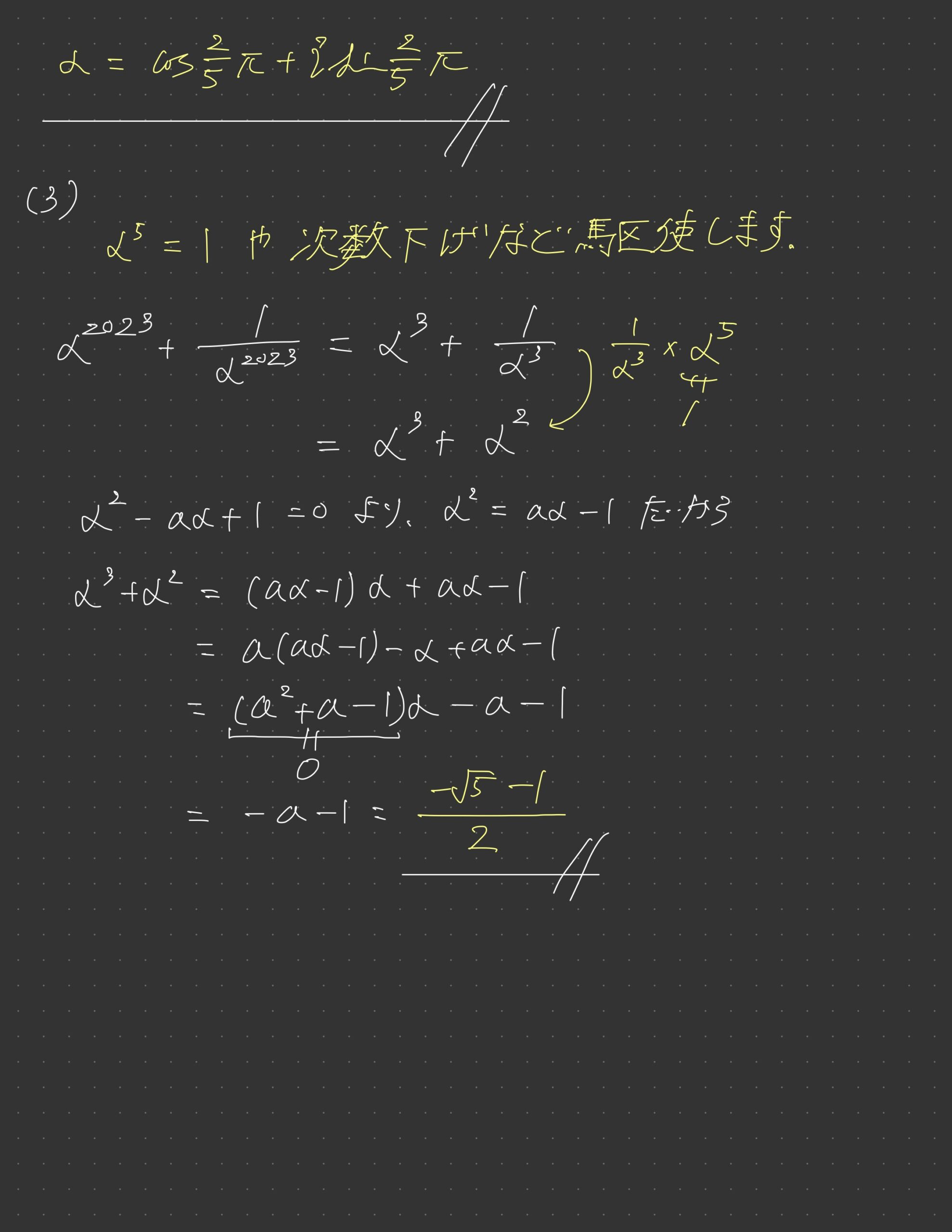
~感想~
(1)は複雑な式でもないので、とりあえず割り算してみるとすんなり0が示せます。
(2)もリード文にもヒントが思いっきり書いてあるので5乗根の話だとすぐ分かるようにされていますね。(もっとも、みんなわかっているでしょうが)
(3)もやはり典型問題ということで、絶対に問題集で一度は見たことがあるような問題。これもみんなできていそう。
第5問




~感想~
これも、計算が少しあるだけで方針はすぐわかるものですね。
しかも(3)で(2)までの正しさもある程度確認が取れるという出血大サービスもいいところな問題で、絶対に落とせない問題になっています。
1~5問まで立て続けにやりやすい問題が並び、第6問は嫌な予感もしますが、ここまでで波に乗っていれば第6問が難しかったら1~5の見直しと割り切れるような気もしますね。
第6問



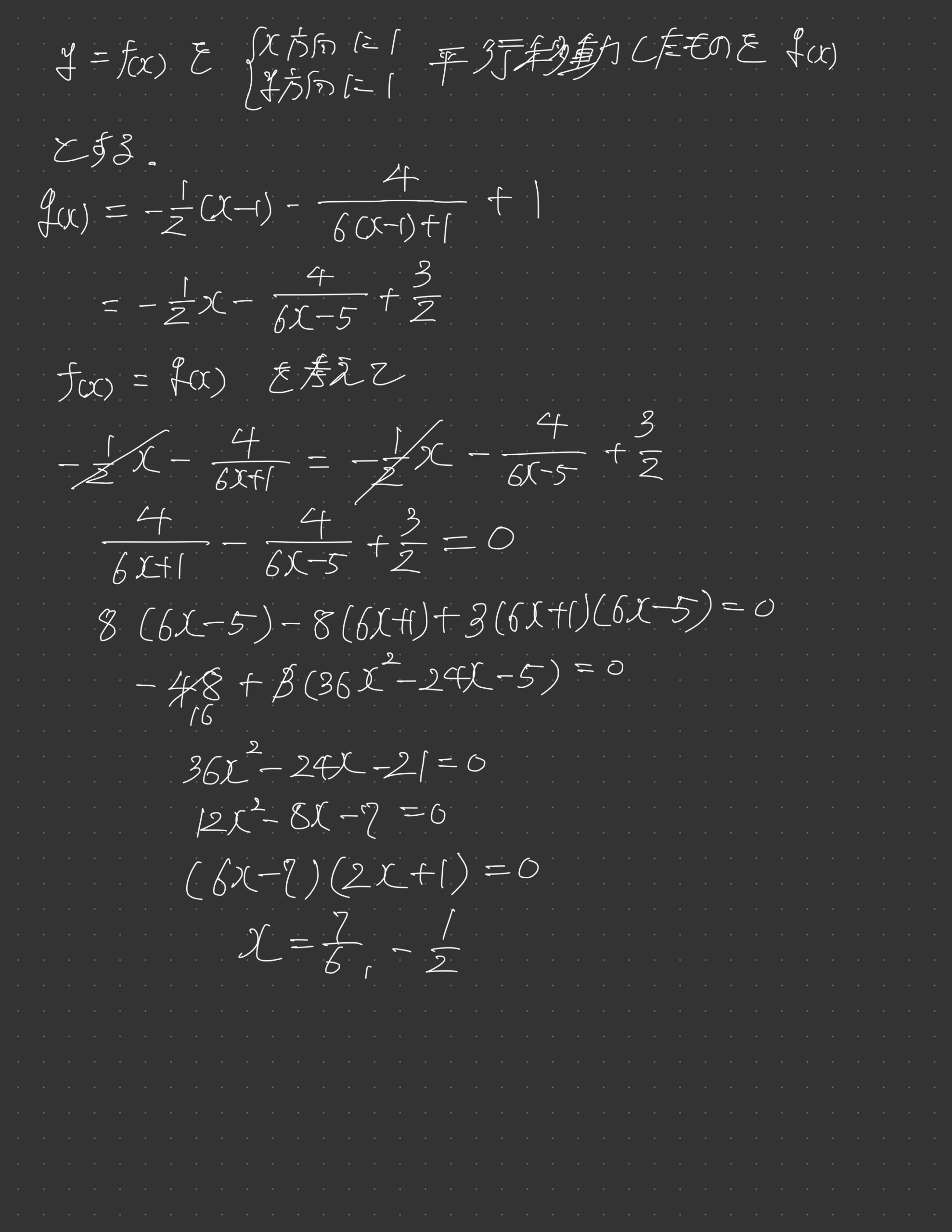
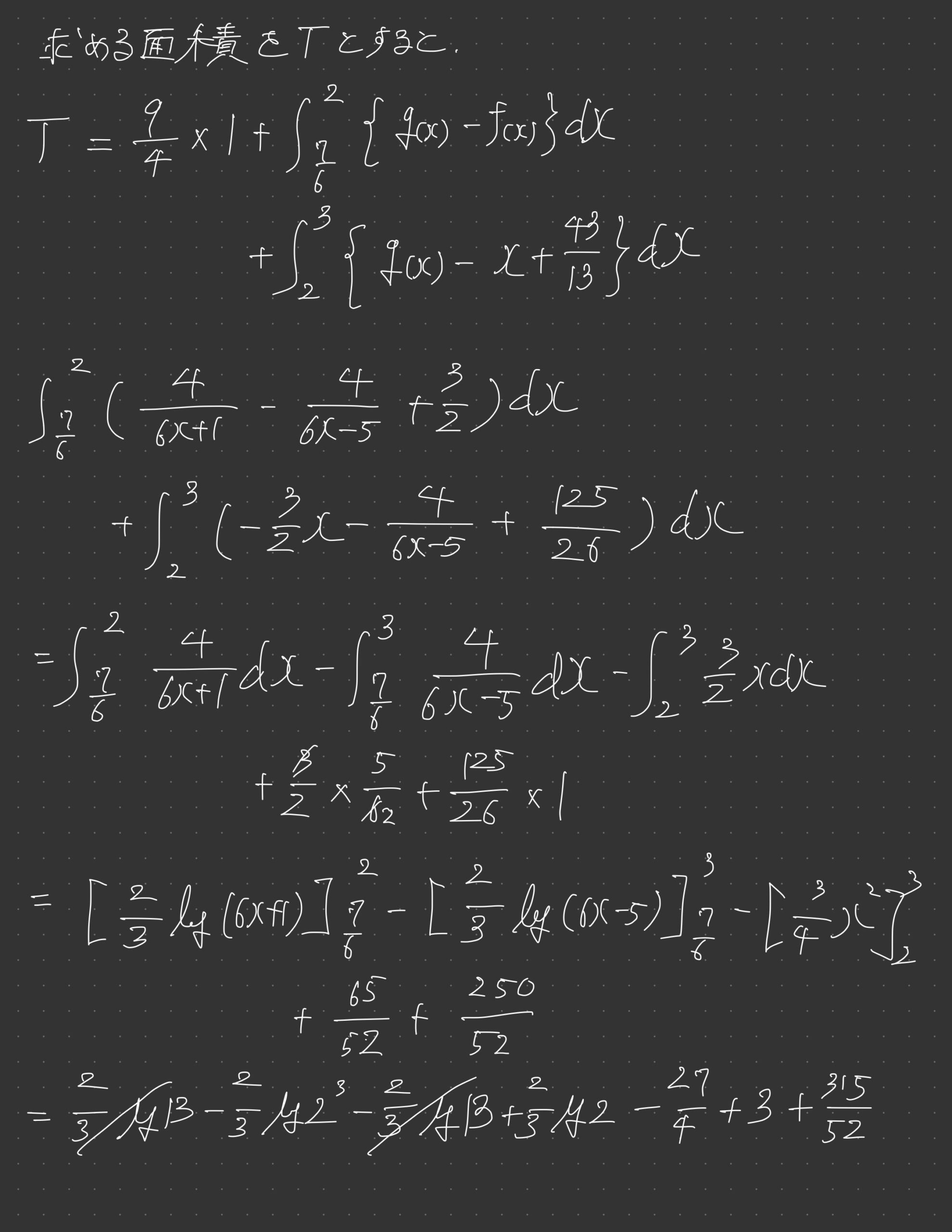
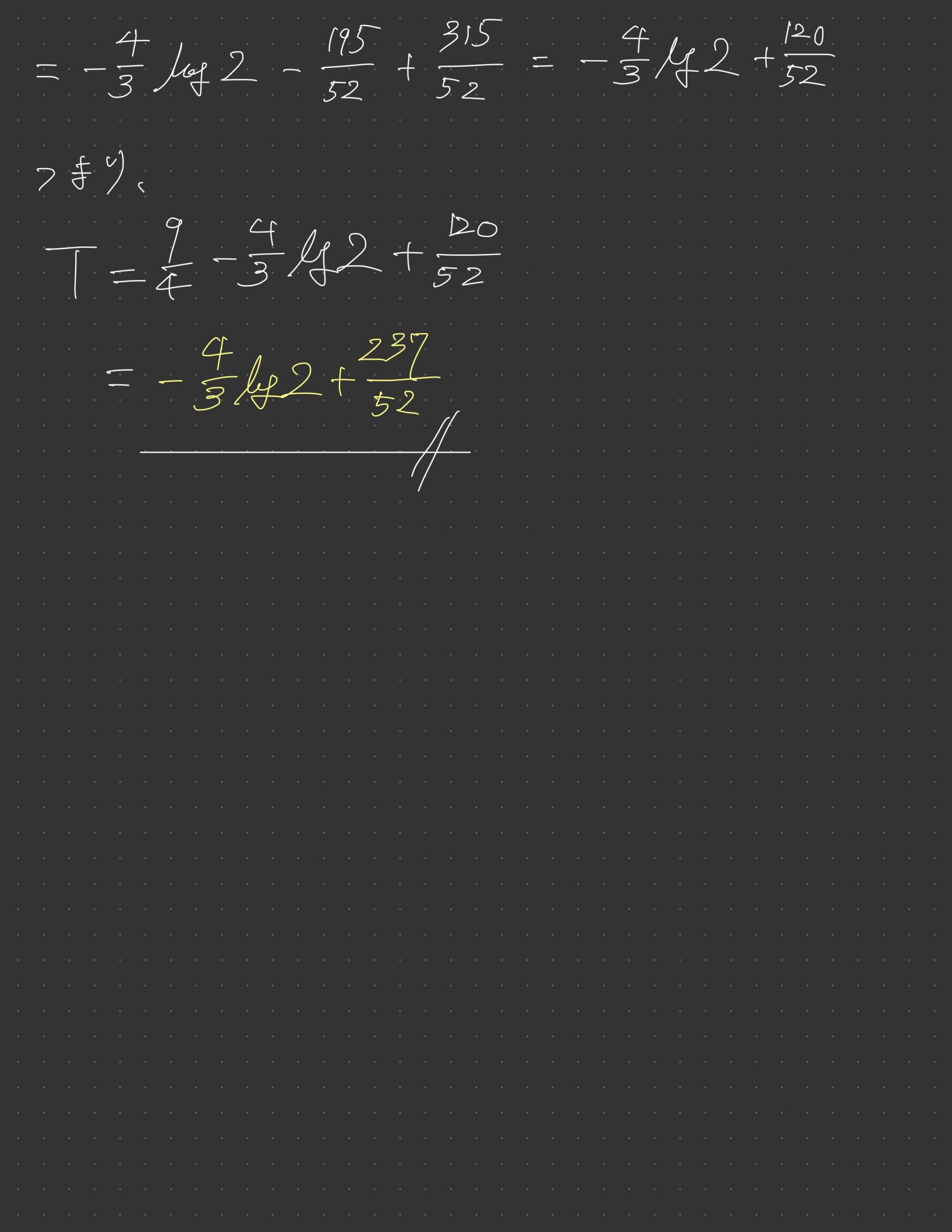
~感想~
(2)は順像法や逆像法でいこうとしましたが、とんでもないことになりました。図形的に棒が動くだけなのは分かっていたので、ざっくりの形はわかりますが、数値がいちいち汚いです。二階微分して上に凸なこともコメントした方がよさそうですが、長くなるのでやめました。
計算が非常に煩雑になり、1~5までと落差もあるため、(1)と(2)の領域の概形を答えるだけ答えておいて、1~5の見直しに使って5完+αを目指すのがよさそうですね。
線分PQは傾きが1となるため、(1)で求めたものが(2)の図示で使う材料となっています。
あとがき
第6問(2)以外は東北大受験生にとっては基本~標準+αといえるものが並びました。
これは数学がある程度以上得意な受験生にとっては5完~6完が目標となる一方で、数学が苦手な受験生には厳しいものだったと思います。超得意と得意な層では差がつかなさそうですが、得意と苦手ではっきり差が出そうです。4完+αで75%くらいが目安になるのでしょうか。


コメント